

Rechenschwäche- |
Was ist Dyskalkulie? |
Symptome |
Qualitative Diagnose |
Therapie-Konzept |
Prävention |
Oberschule/Gymnasium |
|---|
Fortbildungsangebot |
Literaturtipps |
Therapie-Institute |
Dyskalkulie-Links |
Impressum |
Datenschutz |
 |
Telefon 0471/9266844![info[at]rechentherapie.net](logos/mailaddressklein.png) Lothringer Str. 24 27570 Bremerhaven |
Sie sind Besucher: |
Mathematikschwäche (Dyskalkulie) in der Oberschule oder AusbildungAuf weiterführenden Schulen und in der Lehre können grundlegende Verständnislücken
|
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
Die Ursachen dieser Störungen sind so vielschichtig wie die Fehler selbst.Mögliche Entstehungsgründe können sein:• eine Auffassung von Mathematik als purer Handlungsanweisung, deren Gehalt nie wirklich begriffen wurde • Wissens- und Verständnislücken, die durch äußere Faktoren bedingt sind • falsche Vorstellungen von den mathematischen Operationen • sog. "Betriebsunfälle" beim Aufbau des Mengen- und Zahlbegriffs bereits in der Grundschule • eine Dyskalkulie, die nicht behandelt wurde Aber: Die häufig vorkommende Interpretation von chronischem Versagen in Mathematik als Ausdruck einer allgemeinen genetisch bedingten Minderbegabung oder auch (bei Mädchen) als geschlechtsspezifisches Anlagedefizit konnte bisher in wissenschaftlichen Untersuchungen nicht bestätigt werden. Mathematik ist und bleibt eine Kulturtechnik. Eine resignative Haltung bei chronischen Schwierigkeiten in Mathematik ist daher genauso verfehlt wie deren vordergründige Interpretation als Anhäufung von Flüchtigkeitsfehlern oder schlicht Faulheit, dem mit vermehrtem Pauken abzuhelfen wäre. So können generelle Verständnisprobleme in den Grundrechenarten durch eine Rechenstörung auch sehr viel später noch gravierende Auswirkungen zeitigen, ohne dass Rechenschwäche (Dyskalkulie) im engeren Sinne beim Grundrechnen vorliegen muss. |
|||||||||||||||||||||||||
Was tun gegen eine verschleppte Rechenstörung?Wegen ihres folgerichtigen und strengen Aufbaus verzeiht die Mathematik auch kleinere Wissens- und Verständnislücken kaum. Im schulischen Unterricht bleiben solche Lücken zunächst oft unerkannt, da solche Schüler durch einfaches Auswendiglernen des Stoffes für die nächste Lernzielkontrolle anfangs noch zu ganz passablen Leistungen kommen können. Diese "Lernstrategien" werden aber untauglich, je weiter der Stoff voranschreitet. Die Lücken vergrößern sich nämlich beständig – spätestens in der Ausbildung treten diese dann offenkundig zutage. Das führt i.d.R. zu dem verschärften Versuch, mit individuellen Lösungsstrategien im Mathematikunterricht trotz allem zu "überleben", obwohl man wenig versteht. Diese Strategien bestehen dann meist in einer willkürlichen Kombination von Rechenregeln und mathematischen Gesetzen, die man irgendwann in seiner "mathematischen Laufbahn" schon mal gehört hat, ungeachtet dessen, ob sie zur aktuellen Aufgabenstellung passen. So versteht der Schüler weder die Aufgabenstellung noch den Inhalt des mathematischen Gesetzes, das er zu deren Lösung heranzieht.So wird die Bearbeitung einer Schulaufgabe leicht zum Lotteriespiel. Eine Qualitative Lernstandsanalyse ermittelt, an welchen Stellen im mathematischen Aufbau das Verständnis der Zusammenhänge nicht vorhanden oder schwammig ist, lückenhaft wird und Aufbauendes nicht mehr verstanden werden kann. Der Lösungsansatz des Schülers bei der Bearbeitung der mathematischen Aufgabenstellung gibt Aufschluss über sein "individuelles mathematisches Denken" und damit über seine Missverständnisse und Lücken. Vordergründig scheint es immer der aktuelle Lernstoff zu sein, an dem man mal wieder gescheitert ist, tatsächlich sind die Schwierigkeiten oftmals fundamental und liegen weit zurück. Mit einer speziell für diese Schwierigkeiten angepassten Diagnostik unseres Instituts lassen sich die Defizite inhaltlich genau bestimmen und ihre qualitative Bedeutung für den Aufbau des mathematischen Gedankengebäudes angeben. So kann geklärt werden, ob die unbefriedigenden Leistungen in Mathematik auf mangelhaft entwickeltes mathematisches Denken zurückzuführen sind, ob eine Dyskalkulie vorliegt oder nur einzelne kleine Lücken im Stoff vorhanden sind. Eine frühzeitige differenzierte Diagnose der Sachlage ist dringend angeraten, da eine rechtzeitige Förderung nicht nur für die schulische Entwicklung, sondern auch für das Wohlbefinden des Jugendlichen und seine gesunde Persönlichkeitsentwicklung, notwendig ist. Herkömmliche Schulleistungstests sind hierfür wenig aussagekräftig, da sie die qualitativ ganz verschiedenen Defizite in der Regel einfach (als nicht ausreichende Punktzahl) addieren - und damit gleichmachen. Unsere Lernstandsanalyse findet in Einzelsitzung statt und ermittelt ein individuelles qualitatives Fehlerprofil, das im Bedarfsfall die solide Grundlage für den speziellen mathematischen Aufbaukurs oder die eventuell nötige Therapie bildet. Das Fehlerprofil und seine Ergebnisse werden in einem ausführlichen Beratungsgespräch erläutert. |
|||||||||||||||||||||||||
Lernziel: "mathematisches Denken" wirklich erlernen und verstehen |
|||||||||||||||||||||||||
Dazu einige Beispiele:
|
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
| Neuaufbau mathematischen Denkens Unseren Therapiebausteinen liegt ein bewährtes institutseigenes Programm zu Grunde. Es dient als Leitfaden und Rückgrat für den Neuaufbau mathematischer Gedankengänge vom Beginn der Grundschule bis zur 10. Klasse des Gymnasiums. Unabhängig davon, ob es sich um eine Rechenschwäche handelt, oder ob grundlegende Schwierigkeiten im Umgang mit dem höheren mathematischen Stoff zu diagnostizieren sind, bildet die Erfassung und richtige Deutung der vorfindlichen Fehlerstrukturen den Ausgangspunkt für die Auswahl der zu bearbeitenden Module. Das systematische Vorgehen anhand dieser Bausteine soll es den Schülern ermöglichen, das Wesentliche mathematischer Gedanken wirklich erfassen und einordnen zu können. (Auf Basis eines Textes des Mathematischen Instituts zur Behandlung der Rechenschwäche - München ©) |
|||||||||||||||||||||||||
Themen der Therapiebausteine:
|
|||||||||||||||||||||||||
 |
Hier gibts einen Funktionsplotter für alle, die z.B. in der Oberschule mit Funktionen "auf Kriegsfuss" stehen. | ||||||||||||||||||||||||
| Wer sind wir? Das Zentrum für Rechentherapie therapiert seit 2005 Kinder und Jugendliche im Elbe-Weser-Dreieck, in Bremerhaven, Cuxhaven und Zeven. Die Mitarbeiter des Instituts (Psychologen, Pädagogen, Mathematiker) befassen sich aber aufgrund ihrer Mitarbeit in anderen renommierten Instituten in ganz Norddeutschland schon sehr viel länger mit der Behandlung und weiteren Erforschung der Dyskalkulie. Sie verstehen sich als Ansprechpartner für alle Schwierigkeiten im Bereich des Rechnens und mathematischen Denkens, für Kinder und Jugendliche bei denen alles Üben und Pauken sich als sinnlos erwiesen hat, und wo die Möglichkeiten schulischer Förderung nicht ausreichen. Der therapeutischen Arbeit und ihrem Erfolg liegt ein erprobtes und bewährtes institutseigenes Therapieprogramm zu Grunde. Telefon: 0471 9266844 |
|||||||||||||||||||||||||
| Zurück zum Anfang | Literatur | Unsere Standorte | Datenschutz | Impressum | ||||
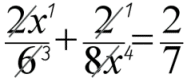
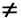 5xy
5xy
